Mohr’s circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor.
That’s why I never understood what it was when I was getting my undergraduate degree. For any real geotechnical engineers, you don’t need to read this article. See you next week.
Mohr’s circle is very simple. In 1882, Christian Otto Mohr developed the graphical method for analyzing stress known as Mohr’s circle and used it to propose an early theory of strength based on shear stress.
Okay, let’s visualize an element of soil in the ground. A piece of dirt if you wish. This soil element is below level ground. The soil element is under a vertical load (i.e., a vertical stress), symbolized by σv. There is also a horizontal stress. In a normally consolidated soil, the vertical stress is greater than the horizontal stress, symbolized by σh. In this case, the ratio of horizontal to vertical stress is called coefficient of Earth pressure at rest, and is symbolized as K0, and K0 = σh / σv. At any depth Z, the vertical pressure, σv = γZ. Where γ is the unit weight of soil.
The value of K0 depends upon the relative density of soil, and the process by which the soil deposition has taken place. If the process does not involve artificial tamping, the value of K0 ranges from about 0.4 for loose sand to 0.6 for dense sand. Artificial tamping increases the value of K0.
Commonly, K0 is defined by K0 = (1 – sin f’), so for a soil with a 30o friction angle, K0 = 0.5
Where were we, oh yes, Mohr’s circles.
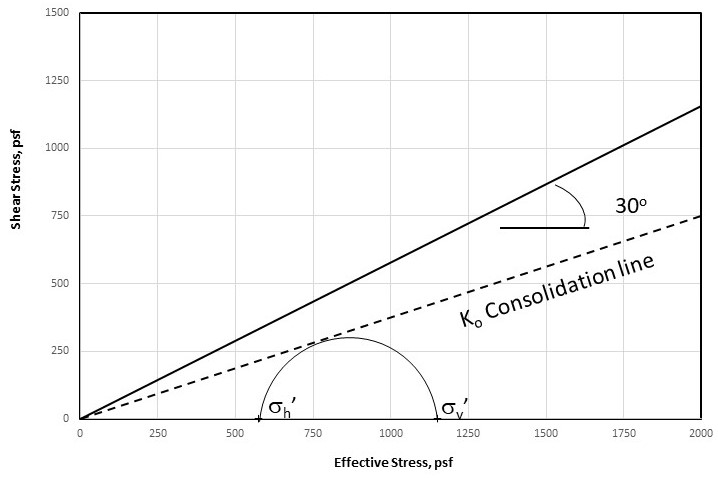
Let’s work out an example, using U.S. Customary Units. Say the soil density is 115 pounds per cubic foot (pcf). The friction angle is 30o. The depth of our soil element is 10 feet.
So, σv = γZ = 115 pcf * 10 feet = 1150 pounds per square foot (psf).
If K0 = σh / σv then σh = K0 * σv
Given K0 = (1 – sin f’), then K0 = (1 – sin 30o) = 0.5 (as already stated), so,
σh = K0 * σv = 0.5 * 1150 psf = 575 psf
And now we can plot this.
Notice the two points on the Mohr circle. They are the vertical and horizontal stresses.
The angle of friction (i.e., the failure envelope) is also plotted. The circle is not touching the failure envelope. It isn’t at failure. It is just in a condition of K0 consolidation. If our little soil element becomes buried deeper (without tamping), the circle will grow, shift to the right, and still touch the K0 consolidation line. Okay, it will be tangent to the K0 consolidation line.
It’s really very simple! And now you know Mohr!

