A lot of times geotechnical engineers speak of a friction angle as if it is simply a strength parameter. But is has a physical meaning.
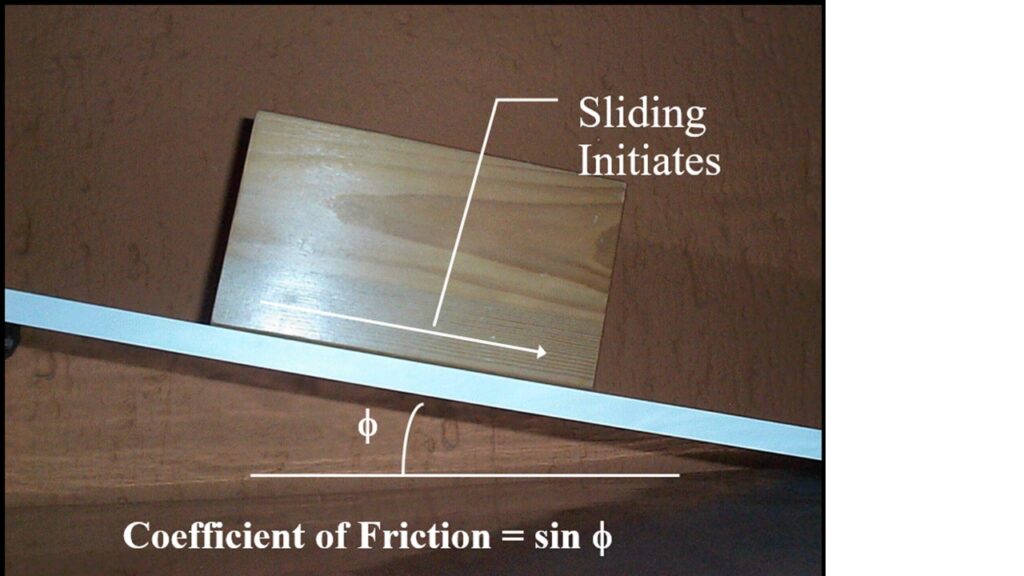
Can you remember the analogy of a sliding block on an inclined plane? You begin with the block in the middle of the plane, with the plane horizontal. You slowly raise one end of the plane, reaching the point where the block just begins to move. This angle is the angle of repose, and also in this case, the angle of friction (denoted f) for the surface (interface) between the block and the plane. The tangent of this angle is equal to the coefficient of (static) friction. In general, the rougher that surface(s) is, the greater the angle you will need to raise the plane, and the greater the angle of repose/friction.
For soils and rock rubble, the angle of repose is only equal to the angle of friction if those materials are loose. If the material is compacted, this relationship is no longer valid.
The friction angle depends on the coefficient of friction, μ, between the two surfaces that will be sliding against each other. The normal stress on the surface is called σn. The shear stress needed to cause movement is τ which is equal to μ × σn. Sometimes this is simplified to state that the force of friction, F, is equal to the product of the normal force, N, and the coefficient of friction, μ, or F = N × μ. Rearranging, this becomes μ = F/N. As stated previously, the tangent of the friction angle is equal to the coefficient of (static) friction; thus, the f is equal to the acrsin (inverse sin) of μ. For soils and rock rubble we generally speak of the internal angle of friction, rather than referring to the friction angle along an interface.

